Flow-based Model
算法思想
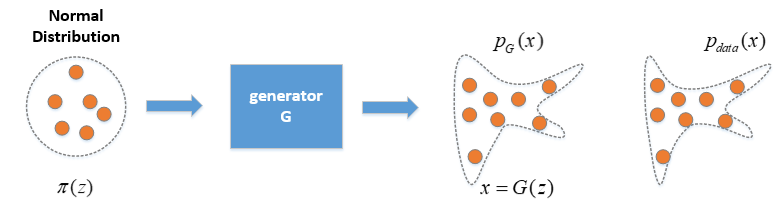
Flow Generative Model的目的是要通过神经网络学习出一个生成器G,变换到一个概率分布PG,也就是输入一个服从简单分布(如正态分布)的z通过Generator G,变换为另一复杂分布下的x。网络最后的优化目标是将x所服从的分布PG尽可能地去拟合实际数据的分布Pdata。
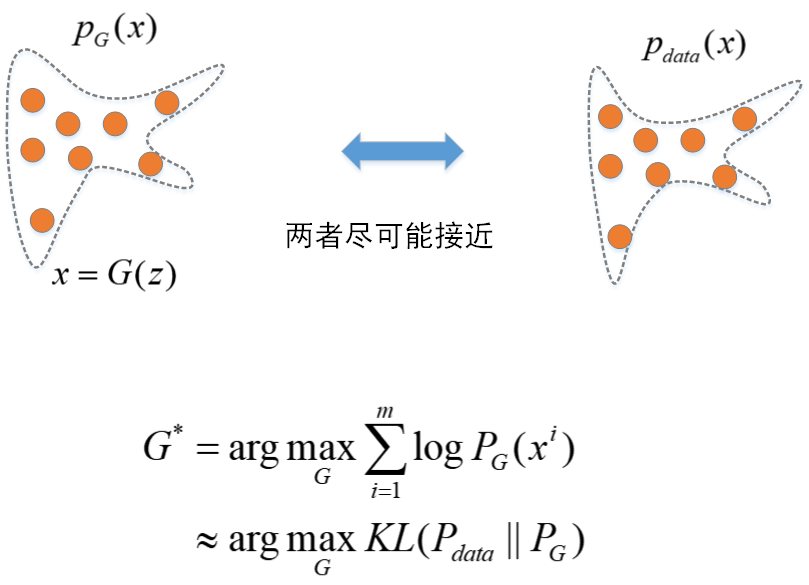
常见的方式是让网络的训练目标最大化实际数据的最大似然估计,换句话说就是让网络学习到的PG与实际数据Pdata尽可能接近(机器学习中用KL 散度衡量两个概率分布的相似性的)。
相关数学知识
雅可比矩阵(Jacobian Matrix)

假设z与x是两个向量(z、x的维度可以不同),z与x满足x=f(z)的变换关系。则可以得到f的Jacobian Matrix。
其中矩阵中每一项是x中的每一元素与z中每一元素的偏微分。i行j列元素可表示为xi与zj的偏微分。
除此之外,我们还可以得到f的反函数z=f^-1^(x)的Jacobian Matrix为zi与xj的偏微分。那么容易推导出Jf与Jf^-1^之间互逆。即反函数对应的Jacobian Matrix互逆。
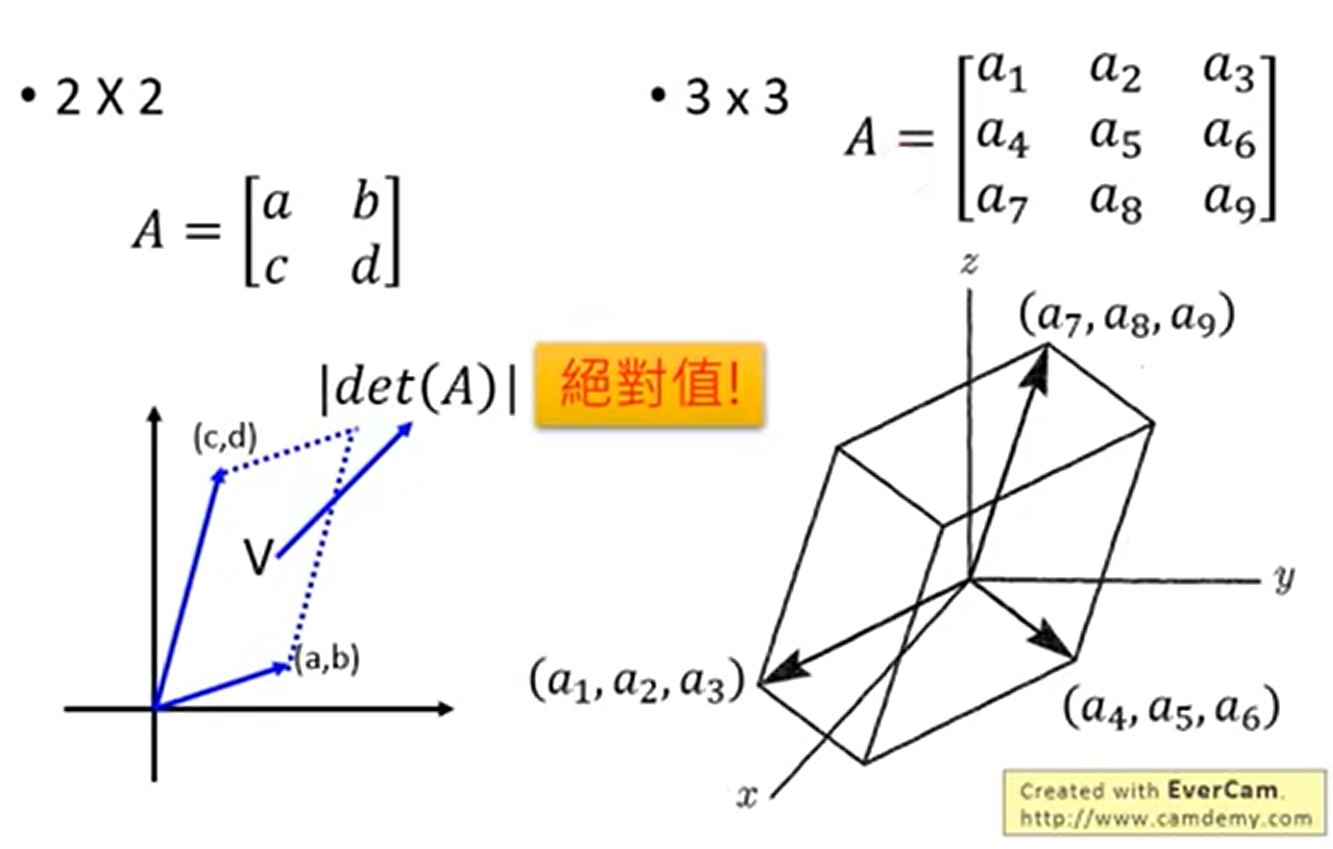
行列式的理解
对于一个矩阵A,我们可以把n维矩阵A的行列式看成是矩阵向量在n维空间中构成图形的“体积”,在二维中可以看做是面积,三维中是体积。这种对于行列式的定义会帮助我们理解接下来的问题。
变量变换定理(change-of-variable theorem)
服从正态分布π的变量z,经过f变换后使其服从分布p,我们如何找出两个分布π(z)、p(x)之间的关系?
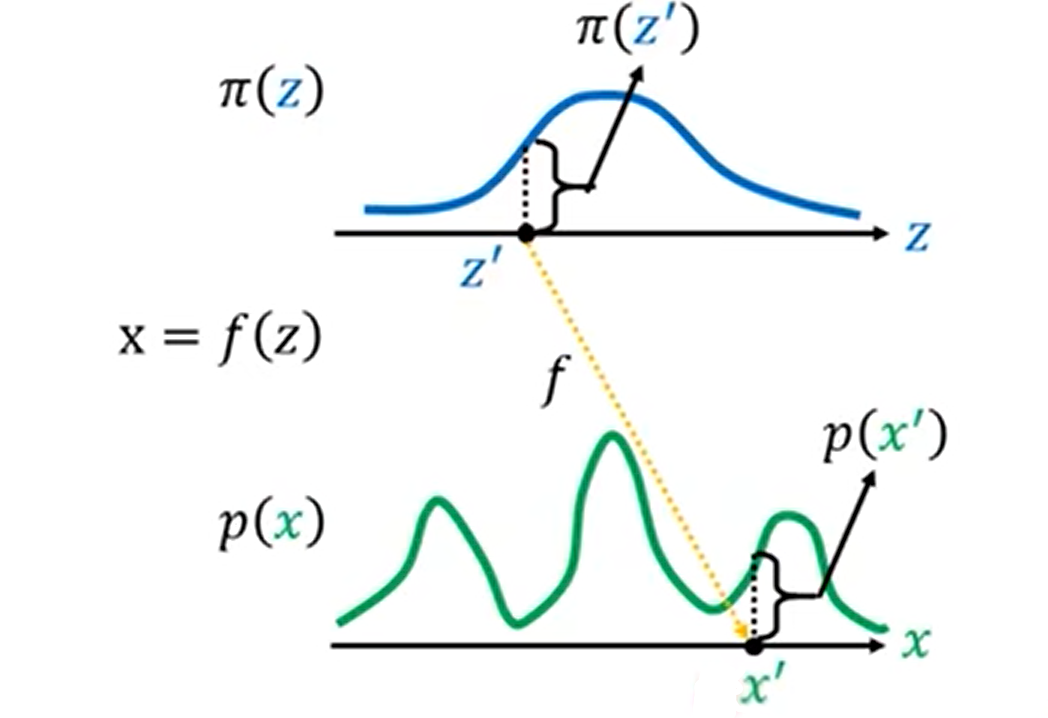
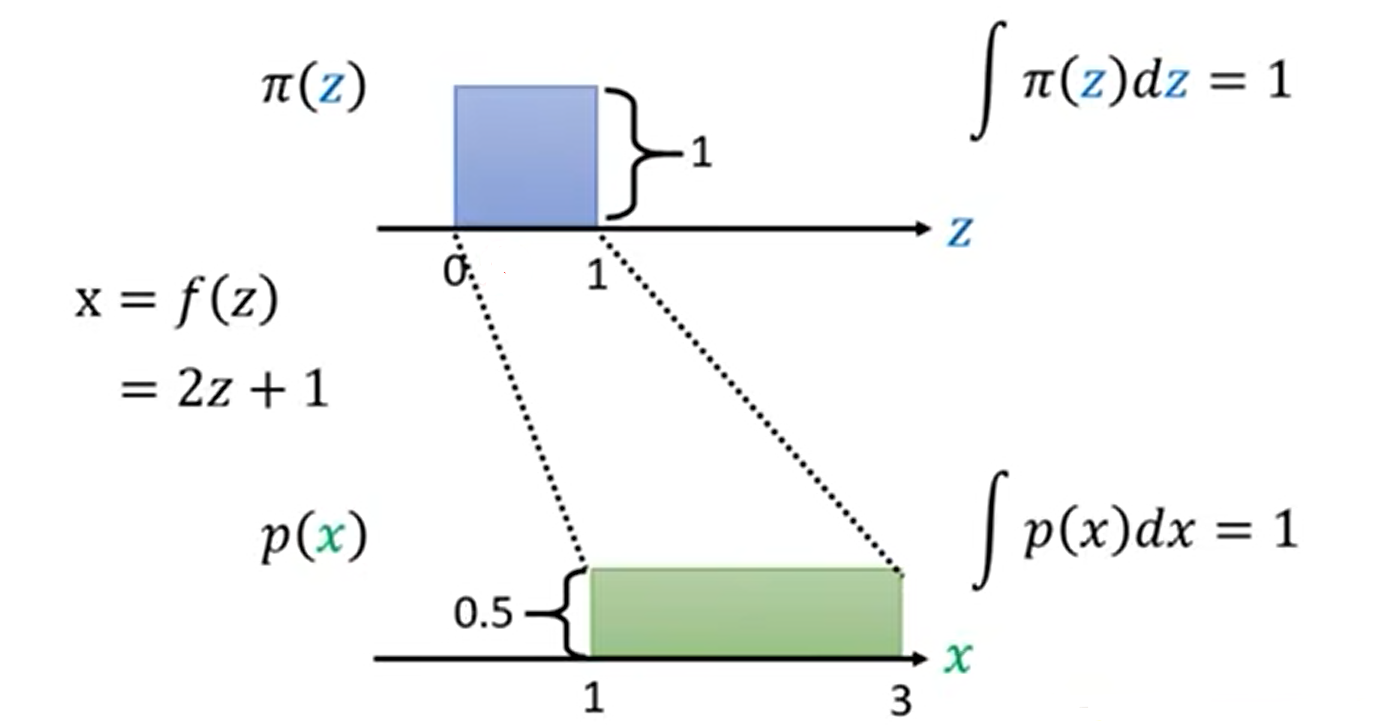
我们假设π分布是在0-1之间的常值,那么根据连续型概率分布函数的性质可以得到其在0-1上的积分为1,那么我们就可以算出,其在0-1上的π(z)=1。接下来,我们通过变换x=2z+1使其变换到分布p上,x的取值变为1-3,同样根据性质,我们就可以算出p(x)=0.5。那么从π(z)到p(x)的对应变换关系为π(z)=1/2*p(x)。
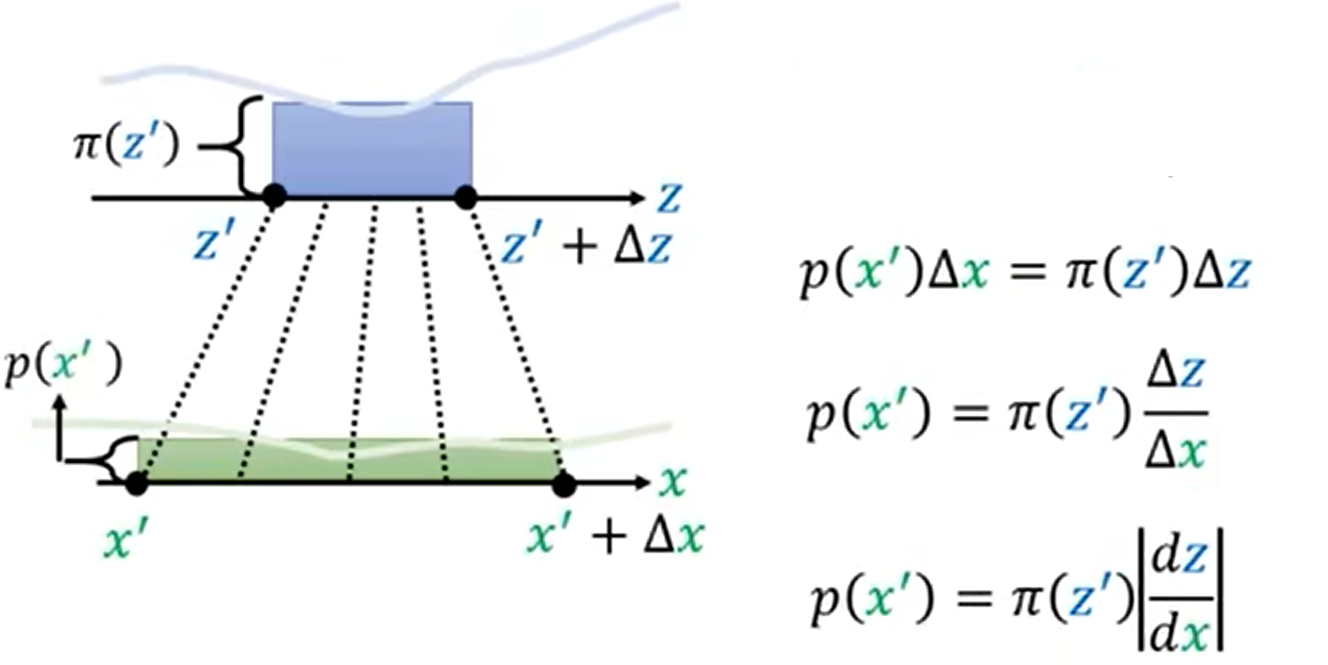
那么,如果π(z)和p(x)是复杂分布情况下,对于(z,z+Δz)变换到(x,x+Δx),从微分的角度可以认为在Δz这个长度内π、p分布是一个常数,那么在这两个分布下的积分是相同的;从几何角度可以表示为π(z)Δz=p(x)Δx,也就是两个矩形面积相等。那么我们就可以得到变换后的概率密度p(x)等于π(z)乘z对x的导数的绝对值。加绝对值的原因是因为z与x的变换规则可能会使z的较大值映射到x的较小值,z的较小值映射到x的较大值,这样z对x的导数就是负数,但对于π(z)与p(x)的大小关系没有影响,因此需要加绝对值。
上述情况我们是在一维空间中讨论,接下来我们把情况推广到高维空间中。以二维空间为例,z、x是二维的向量。我们同样采用微分思想取Δz1、Δz2作为z两个分量的变化量,在这个正方形中我们认为π(z)是相同的,那么把z映射到x的分布中Δx11、Δx21、Δx12、Δx22就是映射后两个向量的坐标。那么在二维空间中这两部分的积分相同,也就可以表示为p(x)|det(X)|=π(z)Δz1Δz2。
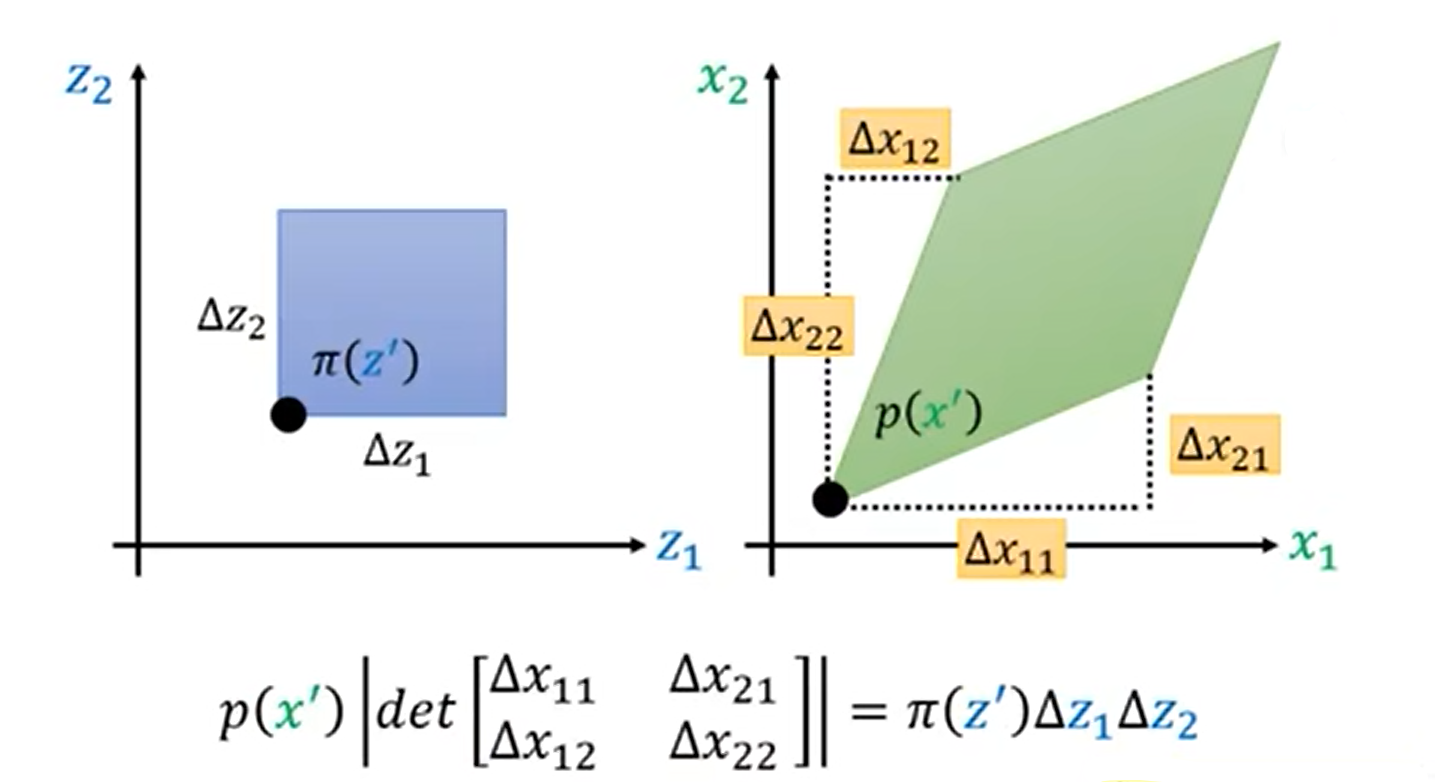
经过整理就可以得到在二维空间上的两分布之间的关系,同时该关系同样可以推广到高维空间中。
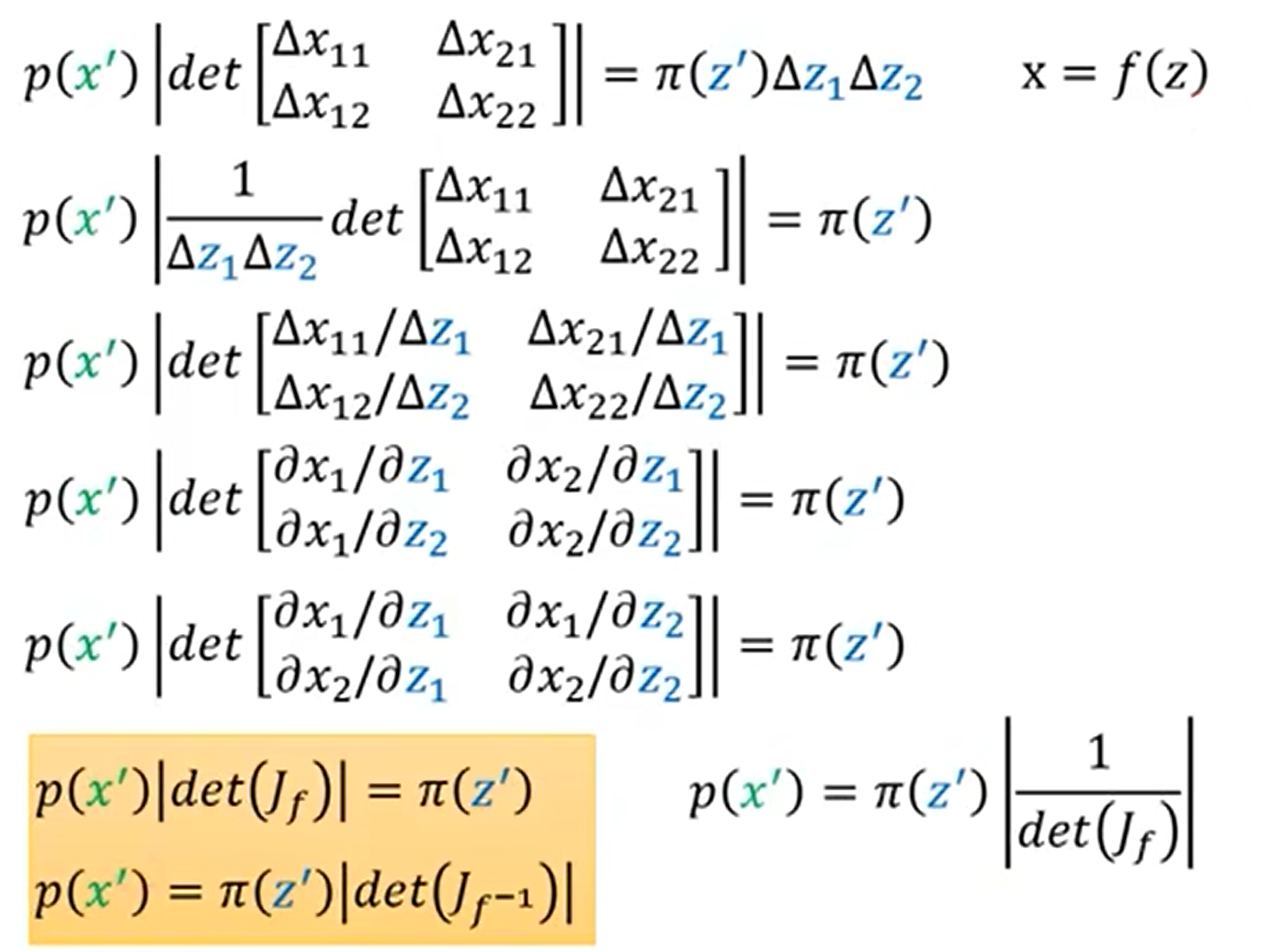
如何Flow
根据上面的推导,我们已经得出来x和z分布函数p(x)与π(z)的关系。之前已经知道,我们的目标就是要最大化PG(x),同时x是z通过generator G变换而来的,因此z可以表示成G的反函数形式,那么我们最后优化的logPG。我们需要对G进行一些限制,保证其:1)能够计算其Jacobian的行列式; 2)可逆。在实际问题中,输入输出往往维数较高,可能有上百甚至上千维,这样在计算Jacobian的行列式以及G^-1^时需要消耗较大的计算量,因此我们在设计generator时,希望能够使行列式以及逆矩阵便于计算。
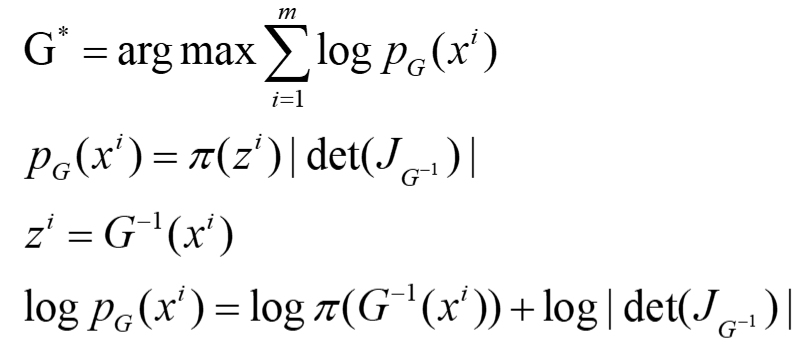
由于上述条件的限制导致G的生成能力很有限。既然一个generator的能力有限,那么可以通过串联多个generator使其能够达到最终需要的效果。

根据其数学推导式可以看到,训练时实际上只需要用到G^-1^就可以了,在正向变换时,我们将G^-1^变换为G就可以了。
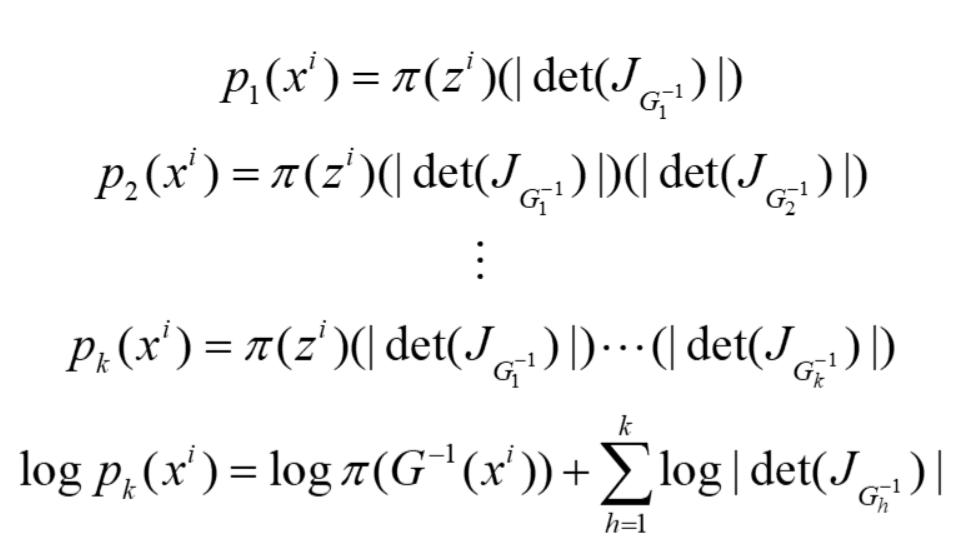
结构设计
我们现在己经可以通过Flow的方式使我们的model具有较强的学习能力。那么我们该如何设计网络使其能够满足上述诸多条件?
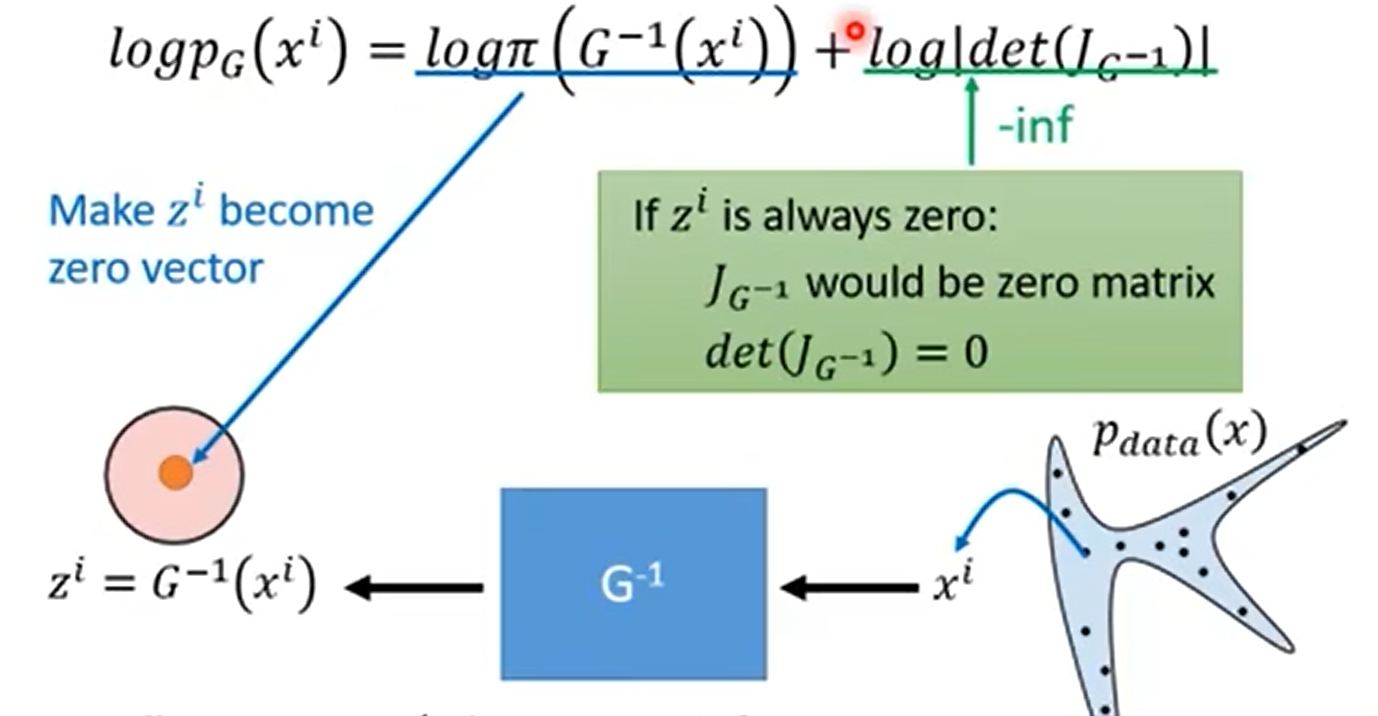
我们的训练目标就是要最大化这个最大似然式。原始分布π是一个标准正态分布,只有当向量为0时,其概率取得最大值,因此G^-1^就要使z成为0向量。如果这样的话,意味着不论x为何值G^-1^都会将其变换为0向量,那么x与z之间不存在函数关系,Jacobian矩阵就为0,行列式也为0,那么第二项就变成了负无穷,这样就无法使整个式子最大化。这样在这个式子中的第一项会让所有的向量向z分布中心集中,同时第二项又限制其不能全为0向量,这就是flow model的目标。
Coupling Layer
之前提到generator G要满足可逆且反函数易得,Jacobian矩阵也要易得。在NICE模型以及Real NVP模型中使用的Coupling Layer可以生成一种generator G满足上述的要求。
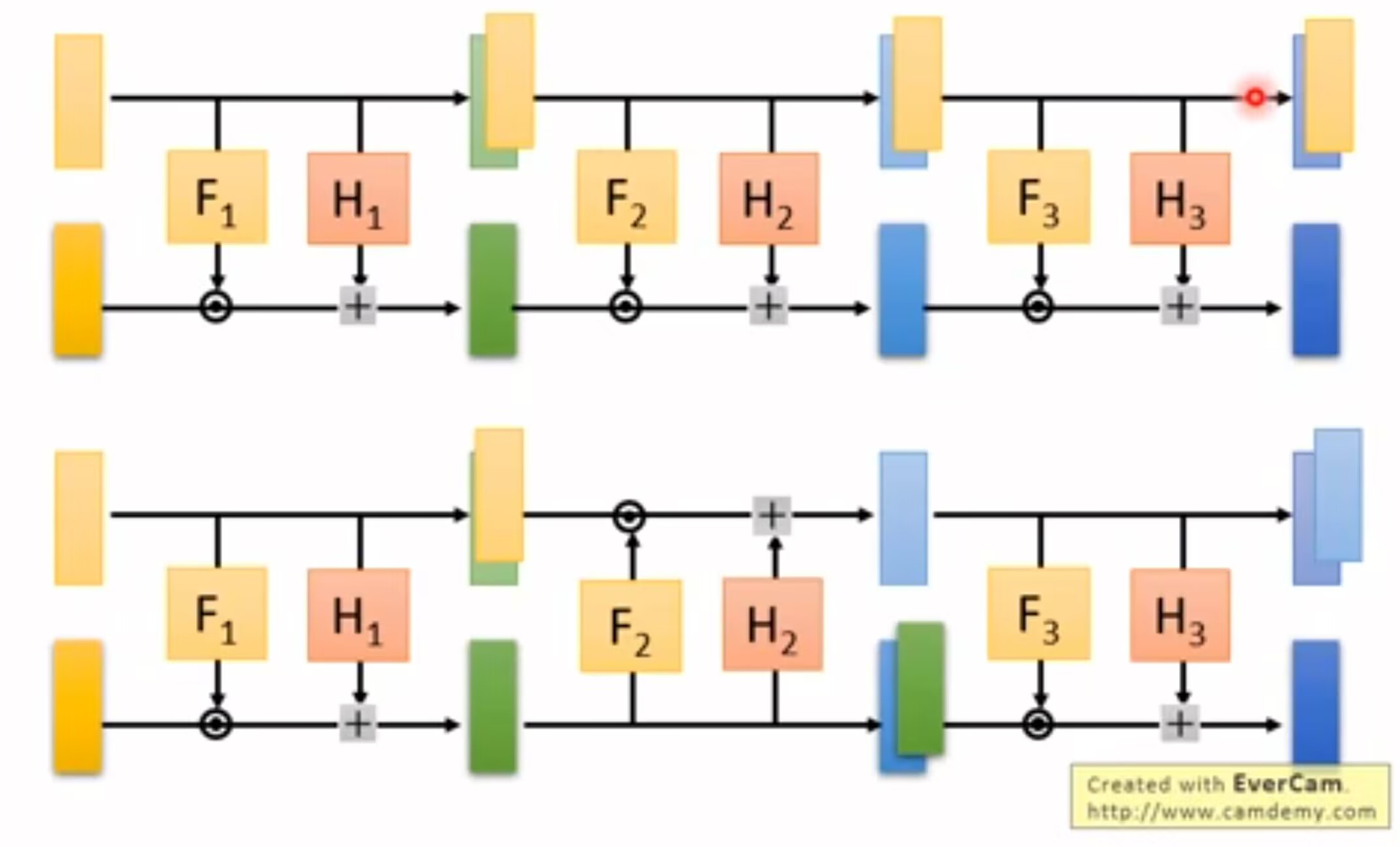
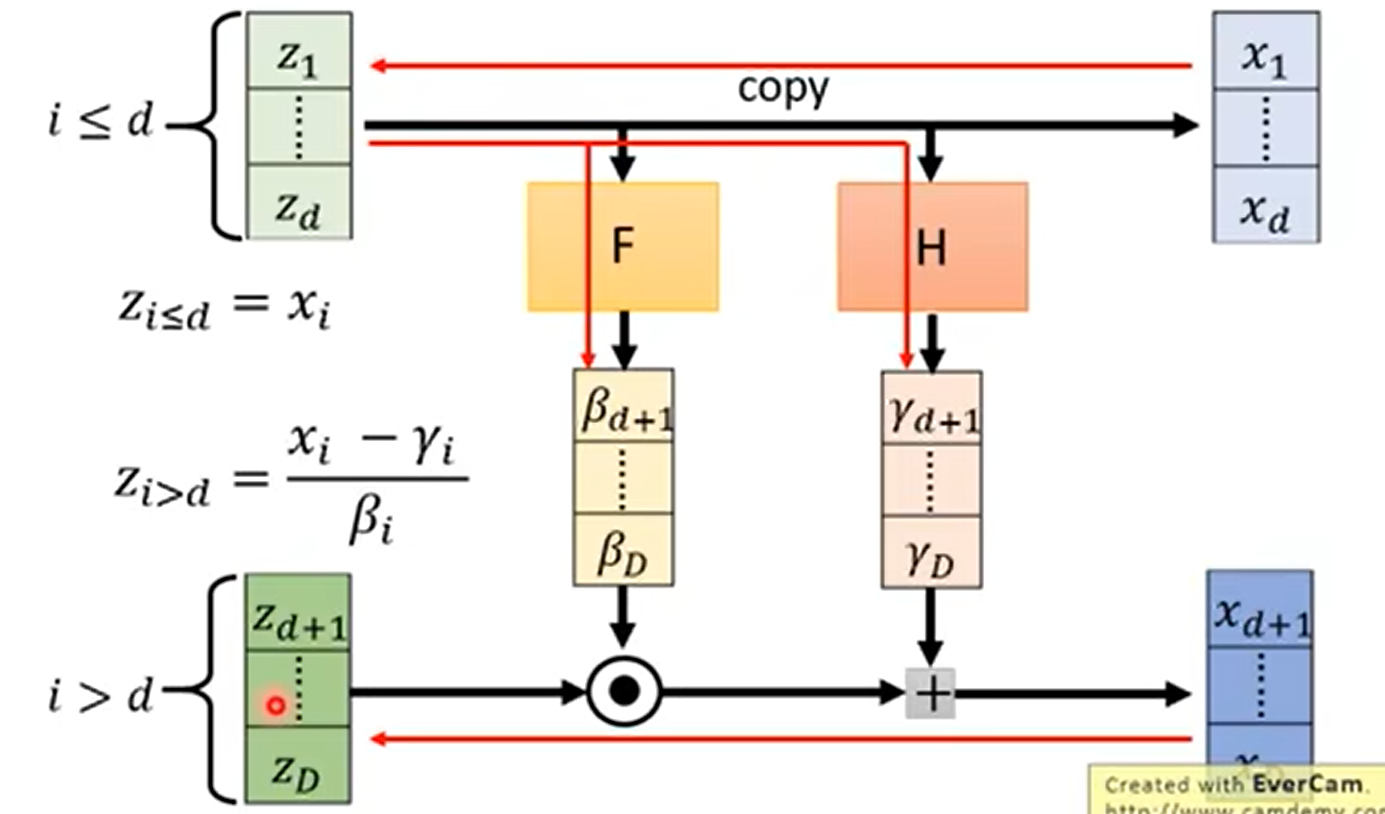
将z向量从1…d维的元素与d+1…D维的元素进行拆分,为了方便叙述,称其为z1、z2。z1直接恒等映射到x1…d。同时将z1通过function F变换为β,通过function H变换为γ,再将z2与β相乘加γ,形成xd+1…D。function F、function H可以是任意的函数,或是神经网络。最后对x进行拼接就形成了x向量。
G^-1^也很容易进行计算,就是将上述过程反向运算,x1…d直接映射为z1,xd+1…D减去γ后再除以β就得到了z2,z1、z2拼接后就得到了z。
Jacobian的行列式计算
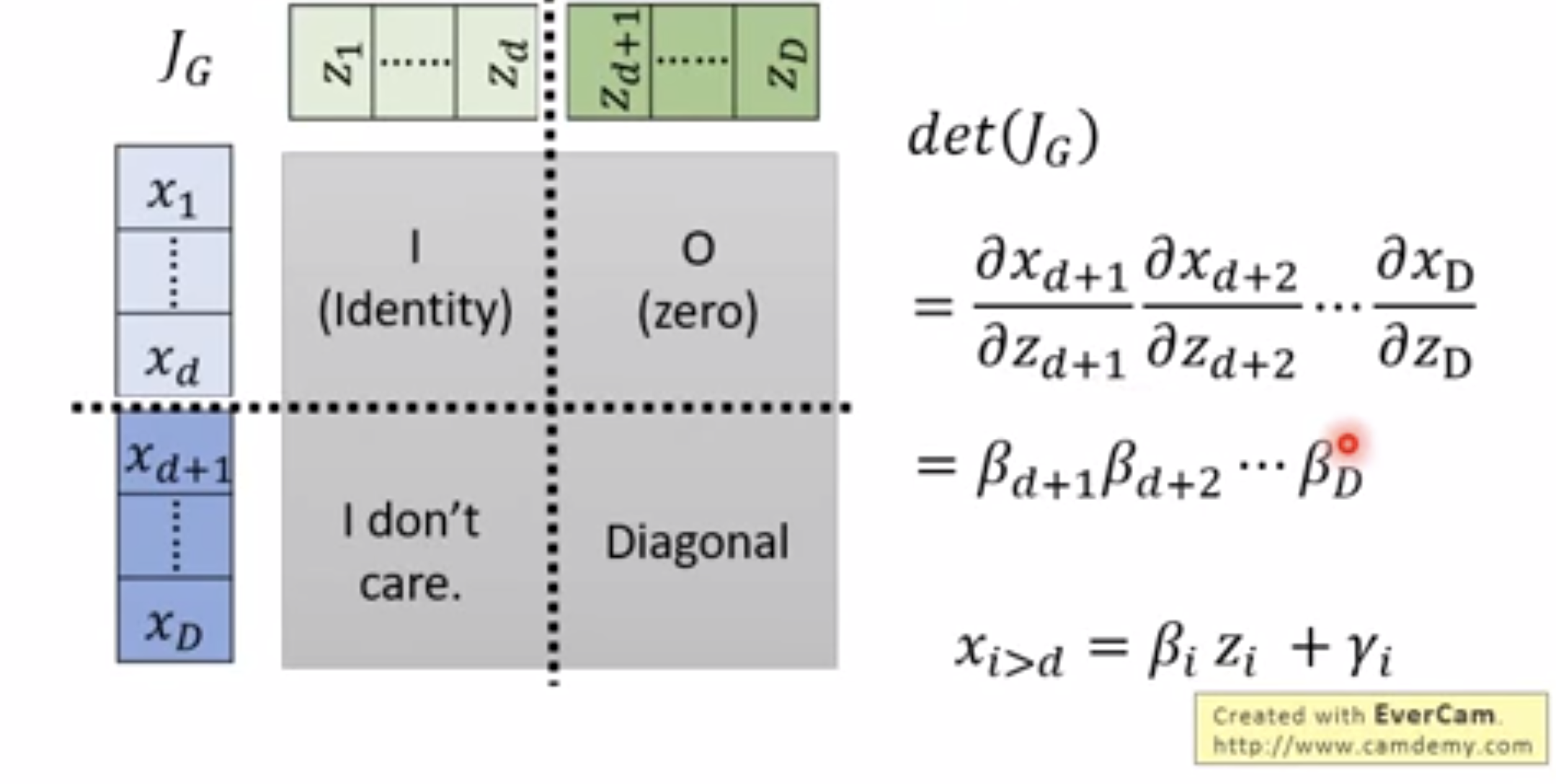
我们已经得到了generator G,如何生成Jacobian?为了叙述方便,还是将x、z的两部分称作x1、x2、z1、z2。
接下来我们来看G的Jacobian生成过程。矩阵的左上部分由于z1、x1是直接映射的,所以这一部分就是单位矩阵。右上部分。由于z2与x1之间没有函数关系,因此这一部分为0矩阵。根据分块矩阵行列式计算定理,左下矩阵的数值对于计算行列式就没有关系了,Jacobian的行列式的值等于右下角的行列式。那么我们只需要计算右下角的行列式即可。根据生成过程可以看出,x2与z2中,只有对应位置的元素有函数关系,因此右下角矩阵是一个对角矩阵,其行列式为其对角元素之积,整个矩阵的行列式也是右下角矩阵对角元素之积,值就等于β之积。
Coupling Layer Stacking
对于Flow形式的Coupling Layer就会出现一个问题,我们将多个Coupling Layer串联后,输出的向量前面的元素与输入完全相同。这显然不是我们想要的形式。要解决这一问题我们实际上只需要进行交叉连接就可以解决这一问题。